Quantum Challenge(or rather puzzle)

　先月(2021年5月)行われたIBM Quantum Challenge 2021に触発され、定言的三段論法(Syllogism)に関連したそれらしい問題を1つ考えてみました。しかしこれは本質的には意味のないもので、わざわざ量子コンピュータを使って解くようなものではありません。ただのパズルであり、頭の体操くらいにしかなりません。それでも良ければやってみてください。

Exercise

　次に示すヴェン図の陰影化(着色、shading)パターンは128種類あります(今回は重なった円の外側を考慮しません)。「あるAはBである。すべてのBはCである。あるCはAではない」のような形式で示される定言的三段論法を表現する場合、Aをq0、q1、q2、q3、Bをq1、q2、q4、q5、Cをq2、q3、q5、q6、それぞれ4つの領域で構成されるものとします。すべての領域は任意で陰影化することができますが、各円の4つの領域すべてを陰影化することはできません。このように規定されたヴェン図の有効な陰影化パターンは109種類となり、19種類は無効な陰影化になります。
　陰影化された領域は、要素が存在しないことを表します。例えば「すべてのAはBである」を表す場合、少なくともq0とq3は陰影化されます。追加でq1またはq2を陰影化することも可能です。
　初期状態では、すべての領域が0と1の可能性があるものとします(アダマールゲートが適用されている状態)。今回の問題は、その状態から有効な109種類の陰影化パターンのみが出力される回路を作成することです。その回路を何度も実行(数万ショット)すれば、少なくとも1回はすべての有効なパターンが出力され(出力される可能性が0%を超え)、何度実行しても無効なパターンは出力されない(出力される可能性が0%である)ということです。

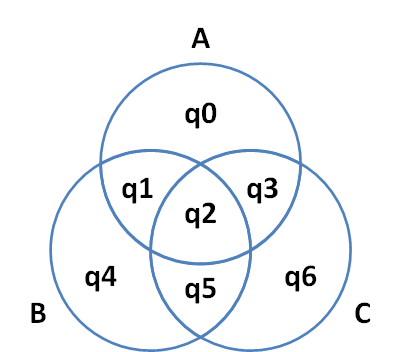
　現代のヴェン図では、陰影化(着色)された領域に要素が存在することを示す場合がありますが、ここではヴェンのオリジナルの表記を踏襲します。

John Venn『Symbolic Logic』London: Macmillan and Co.(1881), Chap. 5 Diagrammatic Representation p. 112

　量子コンピュータ自体がよくわからない場合は、Qiskitのサイトを参考にしてみてください。初心者にもわかりやすく説明されています。但し、情報量もそれなりに多いので「Fundamentals of Quantum Computation Using Qiskit v0.2X Developer」到達レベルくらいまでの基本に絞って学習したい場合は「量子コンピュータを理解するための第一歩」が参考になります。定言的三段論法について知りたい場合は「Syllogism ～ヴォイラー図で見る本当の正しさ～」をお勧めします。

　作成する回路はqc1で、WRITE YOUR CODE BETWEEN THESE LINES – STARTからWRITE YOUR CODE BETWEEN THESE LINES – ENDの間に記述します。OpanQASMで作成しても構いません。

import numpy as np
import sympy as sp
from math import pi, sqrt, log2
from qiskit import *
from qiskit.tools.jupyter import *
from qiskit.visualization import *
from qiskit.quantum_info import Statevector
from qiskit.result import Counts

def correct_sv(qc):
    sv_data = Statevector.from_instruction(qc).data
    
    chk = [0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, \
        1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
        0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, \
        0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
        0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, \
        1, 1, 1, 1, 1, 1, 1, 1]
    
    result = True

    for i in range(128):
        if (chk[i] == 0 and sv_data[i] == (0j)) or (chk[i] == 1 and sv_data[i] != (0j)):
            continue
        result = False
        break

    return result

def calc_score(qcvd):
    qcvdt = transpile(qcvd.copy(), basis_gates=['cx','u'], optimization_level = 2)
    ops = qcvdt.count_ops()
    num_cx = ops['cx']
    num_other = sum(ops.values()) - num_cx
    score = num_cx * 10 + num_other
    return score

def calc_var(qc):
    sv_data = Statevector.from_instruction(qc).data
    return np.var([sp.Abs(sv0) for sv0 in sv_data if sv0 != (0j)])

def get_ideal_counts(qc):
    sv_data = Statevector.from_instruction(qc).data
    c0 = []
    di = '0' + str(int(log2(len(sv_data)))) + 'b'
    
    for k in range(len(sv_data)):
        c0.append(format(k, di))

    d = {k: (round((sp.Abs(sv_data[int(k, 2)])**2) * 1000000)) for k in c0}
    counts = Counts(d)

    return counts

def grade_ex(qc, qc1):
    if correct_sv(qc):
        score = calc_score(qc1)
        score_var = calc_var(qc1)
        counts = get_ideal_counts(qc)
        print('Congratulations 🎉! Your answer is correct.')
        print('Your score(var) is {}({}).'.format(score, score_var))
        display(plot_histogram(counts, (80, 30)))
        print(counts)
    else:
        print('Oops 😕!')
        print('Please review your answer and try again.')

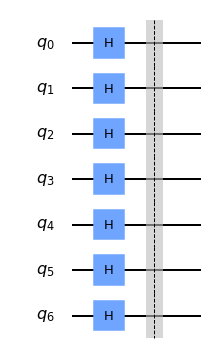
qc = QuantumCircuit(7)
qc.h(range(7))
qc.barrier()
display(qc.draw('mpl'))

qc1 = QuantumCircuit(7)

# WRITE YOUR CODE BETWEEN THESE LINES - START

# qc1 = QuantumCircuit.from_qasm_file('quantum_circuit.qasm')
#
# qc1 = QuantumCircuit.from_qasm_str('''OPENQASM 2.0;
# include "qelib1.inc";
# qreg q[7];
# ''')
#
# qc1.x(0)
# qc1.y(1)
# qc1.z(2)

# No need to measure

# WRITE YOUR CODE BETWEEN THESE LINES - END

qc1.name = 'VD'
qc.append(qc1, range(7))

display(qc1.draw('mpl'))
display(qc.draw('mpl'))

　初期状態(実行直後)は7つの量子ビットすべてにアダマールゲートが適用された状態です(どの領域も０と1になる可能性があることを示しています)。

　この後に作成した回路VD(qc1)を適用します。

　作成した回路が正しいかどうかはgrade_ex(qc, qc1)にて確認できます。スコアとステートベクトルの分散はできるだけ小さい方が望ましいものとします。

grade_ex(qc, qc1)
Congratulations 🎉! Your answer is correct.
Your score(var) is 571(0.00476591320149472).

　IQC2021っぽい😉

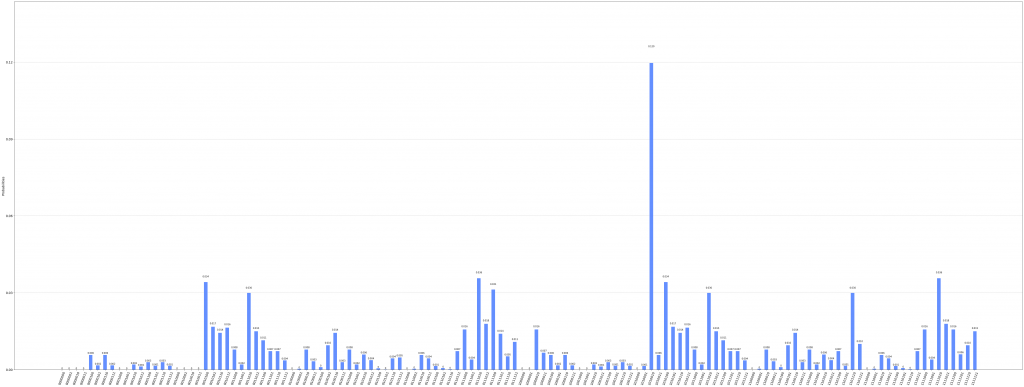
{'0000000': 0, '0000001': 0, '0000010': 0, '0000011': 0, '0000100': 5692, '0000101': 1667, '0000110': 5692, '0000111': 1667, '0001000': 0, '0001001': 0, '0001010': 1953, '0001011': 1228, '0001100': 2846, '0001101': 1423, '0001110': 2846, '0001111': 1423, '0010000': 0, '0010001': 0, '0010010': 0, '0010011': 0, '0010100': 34151, '0010101': 16671, '0010110': 14313, '0010111': 16385, '0011000': 7812, '0011001': 1953, '0011010': 29924, '0011011': 14962, '0011100': 11384, '0011101': 7157, '0011110': 7157, '0011111': 3578, '0100000': 0, '0100001': 335, '0100010': 7812, '0100011': 3265, '0100100': 977, '0100101': 9514, '0100110': 14313, '0100111': 2846, '0101000': 7812, '0101001': 1953, '0101010': 5859, '0101011': 3684, '0101100': 488, '0101101': 42, '0101110': 4395, '0101111': 4757, '0110000': 0, '0110001': 335, '0110010': 5692, '0110011': 4395, '0110100': 1340, '0110101': 560, '0110110': 168, '0110111': 7157, '0111000': 15625, '0111001': 3906, '0111010': 35616, '0111011': 17808, '0111100': 31250, '0111101': 13940, '0111110': 5134, '0111111': 10819, '1000000': 0, '1000001': 0, '1000010': 15625, '1000011': 6530, '1000100': 5692, '1000101': 1667, '1000110': 5692, '1000111': 1667, '1001000': 0, '1001001': 0, '1001010': 1953, '1001011': 1228, '1001100': 2846, '1001101': 1423, '1001110': 2846, '1001111': 1423, '1010000': 0, '1010001': 1340, '1010010': 119696, '1010011': 5692, '1010100': 34151, '1010101': 16671, '1010110': 14313, '1010111': 16385, '1011000': 7812, '1011001': 1953, '1011010': 29924, '1011011': 14962, '1011100': 11384, '1011101': 7157, '1011110': 7157, '1011111': 3578, '1100000': 0, '1100001': 335, '1100010': 7812, '1100011': 3265, '1100100': 977, '1100101': 9514, '1100110': 14313, '1100111': 2846, '1101000': 7812, '1101001': 1953, '1101010': 5859, '1101011': 3684, '1101100': 7157, '1101101': 1423, '1101110': 29924, '1101111': 10044, '1110000': 0, '1110001': 335, '1110010': 5692, '1110011': 4395, '1110100': 1340, '1110101': 560, '1110110': 168, '1110111': 7157, '1111000': 15625, '1111001': 3906, '1111010': 35616, '1111011': 17808, '1111100': 15625, '1111101': 5931, '1111110': 9514, '1111111': 14962}

Sample Circuit

　作成例としてトランスパイルした回路(optimization_level = 0)とそのQASMを提示します。先入観をなくすためチャレンジャーに敬意を表して、元の回路は伏せておきます。

OPENQASM 2.0;
include "qelib1.inc";
qreg q[7];
u(pi/2,0,pi) q[1];
u(0,0,pi/2) q[2];
u(pi/2,0,pi) q[2];
u(0,0,pi/4) q[2];
cx q[0],q[2];
u(0,0,pi/2) q[0];
u(pi/2,0,pi) q[0];
u(0,0,pi/4) q[0];
u(0,0,-pi/4) q[2];
u(pi/2,0,pi) q[2];
u(0,0,-pi/2) q[2];
cx q[2],q[1];
u(0,0,-pi/4) q[1];
cx q[3],q[1];
u(0,0,pi/4) q[1];
cx q[2],q[1];
u(0,0,-pi/4) q[1];
u(0,0,pi/4) q[2];
cx q[3],q[1];
u(0,0,pi/4) q[1];
u(pi/2,0,pi) q[1];
cx q[3],q[2];
u(0,0,-pi/4) q[2];
u(0,0,pi/4) q[3];
cx q[3],q[2];
u(pi,pi/2,pi/2) q[2];
u(0,0,pi/2) q[2];
u(pi/2,0,pi) q[2];
u(0,0,pi/4) q[2];
cx q[3],q[2];
u(0,0,-pi/4) q[2];
u(pi/2,0,pi) q[2];
u(0,0,-pi/2) q[2];
u(pi/2,0,pi) q[3];
cx q[2],q[3];
u(0,0,-pi/4) q[3];
cx q[1],q[3];
u(0,0,pi/4) q[3];
cx q[2],q[3];
u(0,0,pi/4) q[2];
u(0,0,-pi/4) q[3];
cx q[1],q[3];
cx q[1],q[2];
u(0,0,pi/4) q[1];
u(0,0,-pi/4) q[2];
cx q[1],q[2];
cx q[1],q[0];
u(0,0,-pi/4) q[0];
u(pi/2,0,pi) q[0];
u(0,0,-pi/2) q[0];
u(0,0,pi/2) q[1];

u(pi/2,0,pi) q[1];
u(0,0,pi/4) q[1];
cx q[0],q[1];
u(0,0,-pi/4) q[1];
u(pi/2,0,pi) q[1];
u(0,0,-pi/2) q[1];
u(0,0,pi/4) q[3];
u(pi/2,0,pi) q[3];
u(pi,pi/2,pi/2) q[3];
u(0,0,pi/2) q[3];
u(pi/2,0,pi) q[3];
u(0,0,pi/2) q[4];
u(pi/2,0,pi) q[4];
u(0,0,pi/4) q[4];
cx q[5],q[4];
u(0,0,-pi/4) q[4];
u(pi/2,0,pi) q[4];
u(0,0,-pi/2) q[4];
u(pi,0,pi) q[5];
u(0,0,pi/2) q[5];
u(pi/2,0,pi) q[5];
u(0,0,pi/4) q[5];
cx q[2],q[5];
u(0,0,pi/2) q[2];
u(pi/2,0,pi) q[2];
u(0,0,pi/4) q[2];
cx q[1],q[2];
u(0,0,-pi/4) q[2];
u(pi/2,0,pi) q[2];
u(0,0,-pi/2) q[2];
cx q[2],q[1];
u(pi/2,0,pi) q[2];
cx q[1],q[2];
u(0,0,-pi/4) q[2];
cx q[4],q[2];
u(0,0,pi/4) q[2];
cx q[1],q[2];
u(0,0,pi/4) q[1];
u(0,0,-pi/4) q[2];
cx q[4],q[2];
u(0,0,pi/4) q[2];
u(pi/2,0,pi) q[2];
cx q[4],q[1];
u(0,0,-pi/4) q[1];
u(0,0,pi/4) q[4];
cx q[4],q[1];
cx q[2],q[1];
u(pi/2,0,pi) q[2];
u(pi,pi/2,pi/2) q[4];
u(0,0,-pi/4) q[5];
u(pi/2,0,pi) q[5];
u(0,0,-pi/2) q[5];
u(0,0,pi/2) q[6];
u(pi/2,0,pi) q[6];

u(0,0,pi/4) q[6];
cx q[5],q[6];
u(0,0,pi/2) q[5];
cx q[5],q[2];
u(0,0,-pi/4) q[2];
u(0,0,-pi/4) q[6];
u(pi/2,0,pi) q[6];
u(0,0,-pi/2) q[6];
u(pi,pi/2,pi/2) q[6];
u(pi,0,pi) q[6];
cx q[6],q[2];
u(0,0,pi/4) q[2];
cx q[5],q[2];
u(0,0,-pi/4) q[2];
u(0,0,pi/4) q[5];
cx q[6],q[2];
u(0,0,pi/4) q[2];
u(pi/2,0,pi) q[2];
cx q[2],q[3];
u(0,0,-pi/4) q[3];
cx q[6],q[5];
u(0,0,-pi/4) q[5];
u(0,0,pi/4) q[6];
cx q[6],q[5];
u(pi/2,0,pi) q[5];
cx q[6],q[3];
u(0,0,pi/4) q[3];
cx q[2],q[3];
u(0,0,pi/4) q[2];
u(0,0,-pi/4) q[3];
cx q[6],q[3];
u(0,0,pi/4) q[3];
u(pi/2,0,pi) q[3];
cx q[3],q[5];
u(0,0,-pi/4) q[5];
cx q[6],q[2];
u(0,0,-pi/4) q[2];
u(0,0,pi/4) q[6];
cx q[6],q[2];
cx q[6],q[5];
u(0,0,pi/4) q[5];
cx q[3],q[5];
u(0,0,pi/4) q[3];
u(0,0,-pi/4) q[5];
cx q[6],q[5];
u(0,0,pi/4) q[5];
u(pi/2,0,pi) q[5];
cx q[6],q[3];
u(0,0,-pi/4) q[3];
u(0,0,pi/4) q[6];
cx q[6],q[3];
u(pi/2,0,pi) q[6];

　QASMファイル(文字列)を読み込むときにエラーが発生することがあります。その場合はIBM Quantum Composerで読み込んだ後、Qiskit(python)コードに変換してください。

　ステートベクトルの要素がとても小さい(最大と最小の差が大きい)場合、qasm_simulatorの最大ショット数では不足する場合があります。get_ideal_counts(qc)を使えば、理想的な状態で100万回ショットした時の擬似カウントを作成することができます。

　それではチャレンジしてみてください。ですが、その前にもう一度だけ。