KDP Support: Syllogism VD 2nd

　「Syllogism ～ヴォイラー図で見る本当の正しさ～」(第2版、プリントレプリカ版)をお読みくださり、ありがとうございます。編集の都合上、本書では掲載できなかったコンテンツ等を順次アップデートしていく予定です。

46656種類の拡張定言的三段論法を作成する方法

　46656種類の拡張定言的三段論法は次のコードにて作成できます。各項目の意味は次の通りです。

Prmn：前提
Qtf：量化子
Nn：名辞(普通名詞)
Pred：である／ではない
Conc：結論
Valid：有効な拡張定言的三段論法かどうか(推論の妥当性ではありません)
SylType：三段論法の形式(A、B、Cは名詞を表します)

import pandas as pd
import itertools
import re
from pandas.core.common import flatten

def create_syllogism_list():
    quantifiers = ['Some', 'All']
    nouns = ['A', 'B', 'C']
    predicates = ['are', 'are not']
    cols1 = ['Prm1', 'Prm2', 'Conc']
    cols2 = ['Qtf', 'N1', 'Pred', 'N2']
    cols = [''.join(tmp) for tmp in list(itertools.product(cols1, cols2))]

    sentences = list(itertools.product(quantifiers, nouns, predicates, nouns))
    premises1 = premises2 = conclusions = sentences

    docs = itertools.product(premises1, premises2, conclusions)
    docsLstF = [list(flatten(sentence)) for sentence in list(docs)]
    
    df = pd.DataFrame(docsLstF, columns = cols)
    
    df.loc[:, 'Valid'] = True
    
    # Rule 1
    df.loc[(df['Prm1N1'] == df['Prm1N2'])
            | (df['Prm2N1'] == df['Prm2N2'])
            | (df['ConcN1'] == df['ConcN2']), 'Valid'] = False

    # Rule 2
    df.loc[:, 'tmp1'] = df['Prm1N1'] + df['Prm1N2'] + df['Prm2N1'] + df['Prm2N2']
    df.loc[~((df['tmp1'].str.contains(nouns[0]))
            & (df['tmp1'].str.contains(nouns[1]))
            & (df['tmp1'].str.contains(nouns[2]))), 'Valid'] = False

    # 型
    for i in range(3):
        df.loc[(df['{}Qtf'.format(cols1[i])] + df['{}Pred'.format(cols1[i])] == 'Someare'),
               'tmpSylType{}'.format(i)] = df['{}N1'.format(cols1[i])] + 'i' + df['{}N2'.format(cols1[i])]
        df.loc[(df['{}Qtf'.format(cols1[i])] + df['{}Pred'.format(cols1[i])] == 'Someare not'),
               'tmpSylType{}'.format(i)] = df['{}N1'.format(cols1[i])] + 'o' + df['{}N2'.format(cols1[i])]
        df.loc[(df['{}Qtf'.format(cols1[i])] + df['{}Pred'.format(cols1[i])] == 'Allare'),
               'tmpSylType{}'.format(i)] = df['{}N1'.format(cols1[i])] + 'a' + df['{}N2'.format(cols1[i])]
        df.loc[(df['{}Qtf'.format(cols1[i])] + df['{}Pred'.format(cols1[i])] == 'Allare not'),
               'tmpSylType{}'.format(i)] = df['{}N1'.format(cols1[i])] + 'e' + df['{}N2'.format(cols1[i])]

    df.loc[:, 'SylType'] = df['tmpSylType0'] + '-' + df['tmpSylType1'] + '-' + df['tmpSylType2']
    df = df.drop(columns = ['tmpSylType0', 'tmpSylType1', 'tmpSylType2'])
    
    df = df.drop(columns = 'tmp1')
    
    return df

syllst = create_syllogism_list()
count_valid = len(syllst.loc[syllst['Valid'] == True])
count_invalid = len(syllst.loc[syllst['Valid'] == False])
total_docs = count_valid + count_invalid

display(syllst)
print('Valid docs:', count_valid)
print('Invalid docs:', count_invalid)
print('Total docs:', total_docs)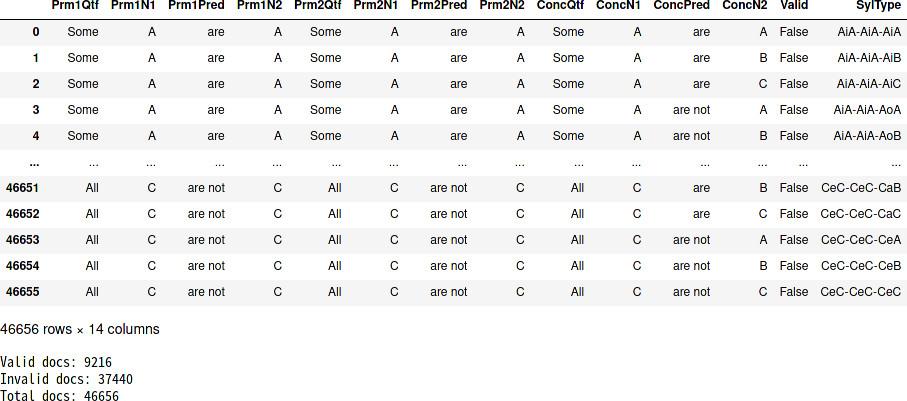

有効な拡張定言的三段論法を抽出する方法

　46656種類の拡張定言的三段論法から有効な拡張定言的三段論法を抽出する場合は次のようにします。

syllst_valid = syllst[syllst['Valid'].isin([True])]
syllst_valid = syllst_valid.drop(columns = 'Valid')
display(syllst_valid)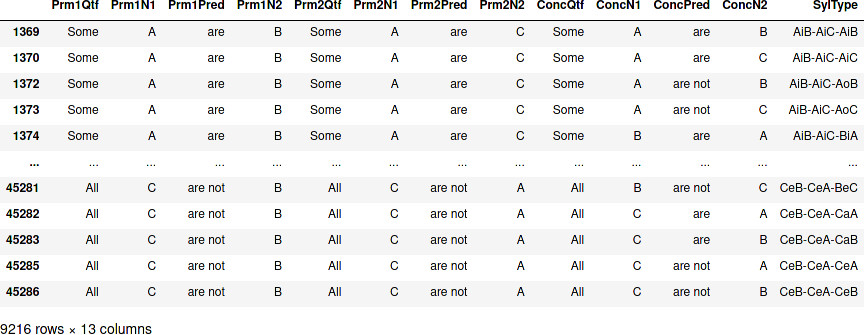

　三段論法の形式がわかっているので、立言の詳細を削除しても問題ありません。

syllst_valid_t = syllst_valid.drop(columns = syllst_valid.columns[range(12)])
display(syllst_valid_t)

伝統的三段論法を抽出する

　有効な拡張定言的三段論法の形式をSPM形式にし、伝統的三段論法の格を設定します。FigNoが0の場合は伝統的三段論法ではありません。また、拡張定言的三段論法には1格、2格のような格の概念がありません。仮想的な格を用いるのであれば1～24の番号を割り当てることが可能ですが、その値に意味がないことは本書で述べた通りです。

def convert_to_spm_notation(doc):
    conc = doc.split('-')[2]
    dic = {'A':'', 'B':'', 'C':''}
    dic[conc[0]] = 'S'
    dic[conc[2]] = 'P'

    m = ''
    if not('A' in conc):
        m = 'A'
    if not('B' in conc):
        m = 'B'
    if not('C' in conc):
        m = 'C'
    
    dic[m] = 'M'
    
    doc_spm = doc.replace('A', dic['A']).replace('B', dic['B']).replace('C', dic['C'])
        
    return doc_spm

def get_mood_num(mood):
    if mood == 'MP-SM-SP':
        return 1
    elif mood == 'PM-SM-SP':
        return 2
    elif mood == 'MP-MS-SP':
        return 3
    elif mood == 'PM-MS-SP':
        return 4
    
    return 0

def set_fig_mood(df) -> None:
    df.loc[:, 'Figure'] = df.loc[:, 'SylTypeSPM'].apply(lambda s: re.sub('[aeio]', '', s))
    df.loc[:, 'Mood'] = df.loc[:, 'SylTypeSPM'].apply(lambda s: (re.sub('[SPM\-]', '', s)).upper())
    df.loc[:, 'FigNo'] = df.loc[:, 'Figure'].apply(get_mood_num)

syllst_valid_t = syllst_valid.drop(columns = syllst_valid.columns[range(12)])
syllst_valid_t.loc[:, 'SylTypeSPM'] = syllst_valid_t.loc[:, 'SylType'].apply(convert_to_spm_notation)
set_fig_mood(syllst_valid_t)
display(syllst_valid_t)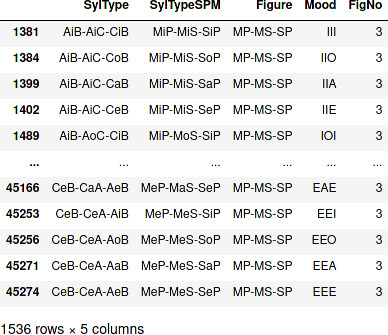

　上記の表は名詞視点で作成されているので1536種類ありますが、伝統的三段論法は格視点で数えるためSPM形式でグループ化する必要があります。

syllst_trad0 = syllst_valid_t[syllst_valid_t['FigNo'].isin([1, 2, 3, 4])]
display(syllst_trad0)

syltype_trad0_spm = [tmp[0] for tmp in syllst_trad0.groupby('SylTypeSPM')]
syllst_trad = pd.DataFrame(syltype_trad0_spm, columns=['SylType'])
syllst_trad.loc[:, 'SylTypeSPM'] = syllst_trad.loc[:, 'SylType']
set_fig_mood(syllst_trad)
display(syllst_trad)

すべての有効な拡張定言的三段論法(9216種類)を検証する

　推論の妥当性を検証するため、最初に次のような検証器を作成します。入力値は「AiB-AiC-CiB」や「MaP-MaS-SaP」のような三段論法の形式です。このサンプルコードではA、B、CやS、P、Mという名詞(記号)にしか対応していませんが、あらかじめ名詞を記号化できる仕組みを導入し、入力された三段論法が有効かどうか確認する機能を追加すれば、汎用的な検証器としても使用可能です。

※この検証器は本書(6.2 検証系の作成)に記載されている検証系(vp_rels)が必要(事前に作成されていることが前提)です。

def verify(doc):
    funcs = get_check_funcs(doc)
    
    chk1 = vp_rels[funcs[0]() & funcs[1]() & funcs[2]()]
    chk1c = vp_rels[funcs[0]() & funcs[1]() & funcs[3]()]
    
    result = 1 # invalid

    if (len(chk1) > 0) and (len(chk1c) == 0):
        result = 0 # valid
    elif len(chk1) == 0:
        result = 2 # invalid(conclusion is not satisfied)
    
    return result

def get_check_funcs(doc):
    sentences = doc.split('-')
    funcs = []

    for sentence in sentences:
        funcs.append(get_check_func(sentence))

    funcs.append(get_check_func(get_neg_sentence(sentences[2])))
        
    return funcs

def get_check_func(sentence):
    s0 = sentence.replace('A', '1').replace('B', '2').replace('C', '3')\
        .replace('S', '1').replace('P', '2').replace('M', '3')

    relmn = 'R' + s0[0] + s0[2]

    if s0[1] == 'a':
        f = lambda : (vp_rels[relmn] == 'B')
    elif s0[1] == 'e':
        f = lambda : (vp_rels[relmn] == 'G')
    elif s0[1] == 'i':
        f = lambda : (vp_rels[relmn] == 'A') | (vp_rels[relmn] == 'B')
    elif s0[1] == 'o':
        f = lambda : (vp_rels[relmn] == 'A') | (vp_rels[relmn] == 'G')

    return f

def get_neg_sentence(sentence):
    if sentence[1] == 'a':
        return sentence[0] + 'o' + sentence[2]
    if sentence[1] == 'e':
        return sentence[0] + 'i' + sentence[2]
    if sentence[1] == 'i':
        return sentence[0] + 'e' + sentence[2]
    if sentence[1] == 'o':
        return sentence[0] + 'a' + sentence[2]

def verify_all(syldf):
    def get_verify_result(doc):
        res = verify(doc)
        if res == 0:
            return 'valid'
        if res == 1:
            return 'invalid'
        if res == 2:
            return 'invalid(conc)'
        
    sylv = syldf.copy(deep = True)
    sylv.loc[:, 'Verify'] = sylv.loc[:, 'SylType'].apply(get_verify_result)
    display(sylv)

    count_verify_valid = len(sylv.loc[sylv['Verify'] == 'valid'])
    count_verify_invalid = len(sylv.loc[sylv['Verify'] == 'invalid'])
    count_verify_invalid_conc = len(sylv.loc[sylv['Verify'] == 'invalid(conc)'])
    total_docs = count_verify_valid + count_verify_invalid + count_verify_invalid_conc

    print('Valid docs:', count_verify_valid)
    print('Invalid docs:', count_verify_invalid)
    print('Invalid(conc) docs:', count_verify_invalid_conc)
    print('Total docs:', total_docs)

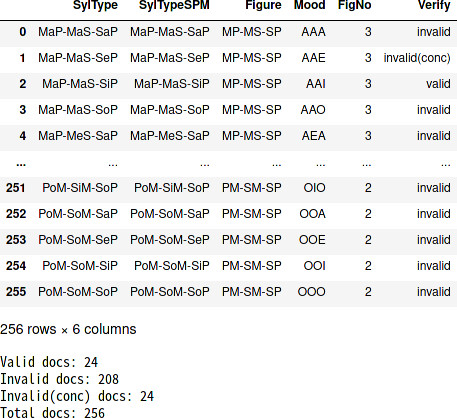
　次のコードを実行すると、推論の妥当性が確認できます。項目Verifyの意味は次の通りです。

valid：推論が妥当
invalid：推論が妥当ではない
invalid(conc)：推論が妥当ではない(結論が成立しない)

verify_all(syllst_valid_t)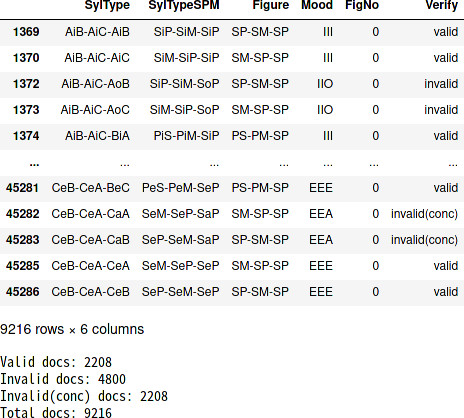

　伝統的三段論法のみ場合は、次のようにします。

verify_all(syllst_trad)